You are here: Home Esoteric Wisdom

Hyper Cubes and Combinatorics

I have discovered a link between hyper cubes and the combinations of partitioned integers.

There are an infinite series of hyper cubes and each one corresponds with the permutations of an integer.

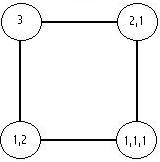
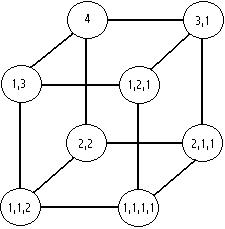
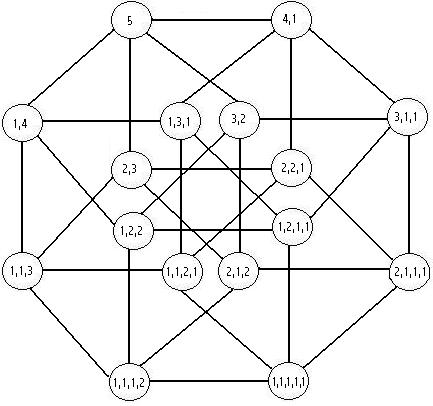
Each circle, in the diagrams below, represents a corner/point on a hyper cube(or on the point, line and square which belong to the same series). Within the circle I have shown the corresponding permutation of the integer partitions.

Each line represents 1 partition either "appearing" or "disapearing" depending on the direction travelled along that line.

If you study the diagrams carefully you will see that the various features are not arbitary and contain some interesting patterns. Each line does indeed correspond with a genuine relationship between 2 permutations of the partitioned integer and these lines are identical to the edges of the corresponding hyper cube.

Integer 1


Integer 2


Integer 3


Integer 4


Integer 5


...and so on for all integer/hypercubes along the infinite series.

You are here: Home Esoteric Wisdom